sábado, 6 de junio de 2015

Tema II (Parábola, Hipérbola)

PARABOLA





En matemáticas, una parábola es la sección cónica de excentricidad igual a 1, resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta. Se define también como el lugar geométrico de los puntos de un plano que equidistan de una recta llamada directriz, y un punto exterior a ella llamado foco. En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en una proyectividad semejante o semejanza.
La parábola aparece en muchas ramas de las ciencias aplicadas debido a que su forma se corresponde con las gráficas de las ecuaciones cuadráticas. Por ejemplo, son parábolas las trayectorias ideales de los cuerpos que se mueven bajo la influencia exclusiva de la gravedad (ver movimiento parabólico y trayectoria balística).

Propiedades Geométricas 


Se denomina parábola al lugar geométrico de los puntos de un plano que equidistan de una recta dada, llamada directriz, y de un punto exterior a ella, llamado foco.
De esta forma, una vez fijados una recta y un punto se puede construir una parábola que los tenga por directriz y foco respectivamente, usando el siguiente procedimiento: Se toma un punto T cualquiera de la recta, se lo une con el foco dado F y a continuación se traza la mediatriz (o perpendicular por el punto medio) del segmento TF. La intersección de la mediatriz con la perpendicular por T a la recta directriz da como resultado un punto P que pertenece a la parábola. Repitiendo el proceso para diferentes puntos T se pueden hallar tantos puntos de la parábola como sea necesario.
De la construcción anterior se puede probar que la parábola es simétrica respecto a la recta perpendicular a la directriz que pasa por el foco. Al punto de intersección de la parábola con tal recta (conocida como eje de la parábola) se le llama vértice de la parábola y es el punto cuya distancia a la directriz es mínima. La distancia entre el vértice y el foco se conoce como distancia focal o radio focal.
Lado Recto

La longitud del lado recto es siempre 4 veces la distancia focal.
Siendo D, E los extremos del lado recto y T, U las respectivas proyecciones sobre la directriz, denotando por W la proyección del foco F sobre la directriz, se observa que FEUW y DFWT son cuadrados, y sus lados miden FW=2FV. Por tanto el segmento DE es igual a 4 veces el segmento FV (la distancia focal).Las tangentes a la parábola que pasan por los extremos del lado recto forman ángulos de 45° con el mismo, consecuencia de que FEUW y DFWT sean cuadrados, junto con la construcción mencionada en la sección anterior. Además, tales tangentes se cortan en la directriz de forma perpendicular, precisamente en el punto de proyección W del foco, propiedades que pueden ser aprovechadas para construir una aproximación geométrica del foco y la directriz cuando éstos son desconocidos.


Semejanza de  todas las parábolas 

Dado que la parábola es una sección cónica, también puede describirse como la única sección cónica que tiene excentricidad e=1. La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.Desafortunadamente, al estudiar analíticamente las parábolas (basándose en ecuaciones), se suele afirmar erróneamente que los parámetros de la ecuación cambian la forma de la parábola, haciéndola más ancha o estrecha. La verdad es que todas las parábolas tienen la misma forma, pero la escala (zoom) crea la ilusión de que hay parábolas de formas diferentes.Un argumento geométrico informal es que al ser la directriz una recta infinita, al tomar cualquier punto y efectuar la construcción descrita arriba, se obtiene siempre la misma curva, salvo su escala, que depende de la distancia del punto a la directriz.

Tangentes a la parábola 

La tangente biseca el ángulo entre el foco, el punto de tangencia y su proyección.
Llamemos F al foco de una parábola, P a un punto cualquiera de la misma y T a la proyección de este sobre la directriz. Sea MP la mediatriz del triánguloFPT, el cual es isósceles por ser iguales las distancias FP y PT, como se ha visto. Luego MP biseca al ángulo FPT, restando verificar si es tangente a la parábola en el punto P.
Sea Q otro punto de la parábola y sea U su proyección en la directriz. Puesto que FQ=QU y QU<QT, entonces FQ<QT. Dado que esto es cierto para cualquier otro punto de la parábola, se concluye que toda la parábola está de un mismo lado de MP, y como la desigualdad es estricta, no hay otro punto de la parábola que toque a la recta MP, esto quiere decir que MP es la tangente de la parábola en P.

Aplicaciones Practicas 

Una consecuencia de gran importancia es que la tangente refleja los rayos paralelos al eje de la parábola en dirección al foco. Las aplicaciones prácticas son muchas: las antenas satelitales y radiotelescopios aprovechan el principio concentrando señales recibidas desde un emisor lejano en un receptor colocado en la posición del foco.
La concentración de la radiación solar en un punto, mediante un reflector parabólico tiene su aplicación en pequeñas cocinas solares y grandes centrales captadoras de energía solar.
Análogamente, una fuente emisora situada en el foco, enviará un haz de rayos paralelos al eje: diversas lámparas y faros tienen espejos con superficies parabólicas reflectantes para poder enviar haces de luz paralelos emanados de una fuente en posición focal. Los rayos convergen o divergen si el emisor se desplaza de la posición focal.




HIPERBOLA









Una hipérbola es el lugar geométrico de los puntos de un plano tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva.

Elementos de la Hipérbola


Eje mayor o real
El eje mayor es la recta de la hipérbola donde pertenecen los focos y los vértices de la misma. Su valor es 2a y es perpendicular al eje imaginario

Eje menor o imaginario
El eje menor o imaginario no tiene puntos en común con la hipérbola. Sin embargo, siempre se cumple que las perpendiculares lanzadas por sus extremos cortan con las perpendiculares lanzadas por los extremos del eje mayor en 4 puntos que pueden servir para trazar las asíntotas.

Asíntotas
Son las rectas r y r' que pasan por el centro de la hipérbola y verifican que se acercan ramas de la misma tanto más cuanto más nos alejamos del centro de la hipérbola.
Las ecuaciones de las asíntotas son: r: y= b/a x r': y = -b/a x

Vértices
Los vértices de una hipérbola son los puntos donde ésta corta a sus ejes.

Focos
Son dos puntos,  F_1 \,y\, F_2, respecto de los cuales permanece constante la diferencia de distancias (en valor absoluto) a cualquier punto, x, de dicha hipérbola.
\vert d(F_1,x)-d(F_2,x)\vert=cte

Centro
Punto medio de los vértices y de los focos de la hipérbola.

Tangentes
La tangente a una hipérbola en cualquier punto de la curva es bisectriz del ángulo formado por los radios vectores de ese punto.

Ecuaciones Parametricas 

Hipérbola abierta de derecha a izquierda:
\begin{matrix} x = a\sec t + h \\ y = b\tan t + k \\ \end{matrix} \qquad \mathrm{o} \qquad\begin{matrix} x = \pm a\cosh t + h \\ y = b\sinh t + k \\ \end{matrix}
Hipérbola abierta de arriba a abajo:
\begin{matrix} x = a\tan t + h \\ y = b\sec t + k \\ \end{matrix} \qquad \mathrm{o} \qquad\begin{matrix} x = a\sinh t + h \\ y = \pm b\cosh t + k \\ \end{matrix}
En todas las fórmulas (h,k) son las coordenadas del centro de la hipérbola, a es la longitud del semieje mayor, b es la longitud del semieje menor.

Publicado por en

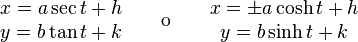
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)